ENSO (cont’d)

Here, we will do a similar analysis than last week, but focussing on the equatorial Pacific. The dominant process along the equator is upwelling, due to the westward tradewinds pushing surface waters northward in the northern hemisphere, and southward in the southern hemisphere due to the earth rotation, resulting in upwelling of cold water from below along the equator. While that upwelling is easily seen in satellite sea surface temperature images, can we see it in drifter tracks?

The global database of drifter tracks is widely available over the internet; the instructions on how to obtain the data for any region are given at the end of this lecture. We have extracted the data for the area and saved as a cvs file.

import pandas as pd
import numpy as np

drifters = pd.read_csv('/home/ocn463-data/woce/drift/pacdrift.gz', compression='gzip', na_values = -999.99)

drifters

	id	month	day	year	lat	lon	sst	u	v	umag	latvar	lonvar	tempvar
0	7702986	3	29.75	1988	2.373	267.958	28.244	-76.816	37.069	85.293	0.000093	0.000151	0.010206
1	7702986	3	30.00	1988	2.442	267.809	28.281	-78.719	32.167	85.037	0.000008	0.000010	0.003204
2	7702986	3	30.25	1988	2.499	267.652	28.063	-78.133	24.650	81.929	0.000045	0.000065	0.010097
3	7702986	3	30.50	1988	2.538	267.505	28.070	-71.856	23.063	75.467	0.000027	0.000038	0.007007
4	7702986	3	30.75	1988	2.589	267.373	28.302	-74.005	27.462	78.936	0.000047	0.000069	0.006161
...	...	...	...	...	...	...	...	...	...	...	...	...	...
2244751	90561	3	30.25	2011	9.961	180.135	27.692	-41.105	-1.209	41.123	0.000006	0.000008	0.004182
2244752	90561	3	30.50	2011	9.964	180.069	27.607	-37.501	3.801	37.693	0.000003	0.000006	0.004396
2244753	90561	3	30.75	2011	9.975	179.988	27.594	-36.597	2.026	36.653	0.000008	0.000010	0.003982
2244754	90561	3	31.00	2011	9.972	179.924	27.704	-36.611	4.784	36.923	0.000022	0.000027	0.004592
2244755	90561	3	31.25	2011	9.994	179.843	27.712	-36.054	11.626	37.882	0.000008	0.000010	0.004258

2244756 rows × 13 columns

There’s a lot more data here than there was in the previous lecture. Let’s make a plot of every 100th track

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(12,12))
ax.plot(drifters['lon'][::100], drifters['lat'][::100], '.')
ax.set_title('Drifter tracks')
ax.set_aspect('equal')

There are some gaps, but we can still see what the currents are like. Let’s make boxes of 1/2 degree latitude and all longitudes, and find the average U and V in each box as well as the standard deviation of them.

NOTE: The code block below takes about 5 or 6 minutes to run on our server, so let’s NOT ALL RUN AT THE SAME TIME

cenlon, cenlat = np.meshgrid(np.arange(165.5, 267.6, 0.5), np.arange(-9.5, 9.6, 0.5))
Umean = np.nan * np.ones_like(cenlon)
Vmean = np.nan * np.ones_like(cenlon)
Ustd = np.nan * np.ones_like(cenlon)
Vstd = np.nan * np.ones_like(cenlon)

for ilat in range(cenlon.shape[0]):
    for ilon in range(cenlon.shape[1]):
        boxlat = np.where(np.absolute(drifters['lat']-cenlat[ilat, ilon]) < 0.5)[0]
        boxlon = np.where(np.absolute(drifters['lon']-cenlon[ilat, ilon]) < 0.5)[0]
        box = np.array(sorted(set(boxlat) & set(boxlon)))
        Umean[ilat, ilon] = np.nanmean(drifters['u'][box])
        Vmean[ilat, ilon] = np.nanmean(drifters['v'][box])
        Ustd[ilat, ilon] = np.nanstd(drifters['u'][box])
        Vstd[ilat, ilon] = np.nanstd(drifters['v'][box])

cenlon

array([[165.5, 166. , 166.5, ..., 266.5, 267. , 267.5],
       [165.5, 166. , 166.5, ..., 266.5, 267. , 267.5],
       [165.5, 166. , 166.5, ..., 266.5, 267. , 267.5],
       ...,
       [165.5, 166. , 166.5, ..., 266.5, 267. , 267.5],
       [165.5, 166. , 166.5, ..., 266.5, 267. , 267.5],
       [165.5, 166. , 166.5, ..., 266.5, 267. , 267.5]])

cenlat

array([[-9.5, -9.5, -9.5, ..., -9.5, -9.5, -9.5],
       [-9. , -9. , -9. , ..., -9. , -9. , -9. ],
       [-8.5, -8.5, -8.5, ..., -8.5, -8.5, -8.5],
       ...,
       [ 8.5,  8.5,  8.5, ...,  8.5,  8.5,  8.5],
       [ 9. ,  9. ,  9. , ...,  9. ,  9. ,  9. ],
       [ 9.5,  9.5,  9.5, ...,  9.5,  9.5,  9.5]])

And now let’s plot then

fig, ax = plt.subplots(2,1,figsize=(15,8), sharex=True)
q = ax[0].quiver(cenlon, cenlat, Umean, Vmean)
ax[0].quiverkey(q, 178, 11, 0.25, '0.25 m/s', coordinates='data')
ax[0].set_ylabel('Latitude')
ax[0].set_xlabel('Longitude')
ax[0].set_title('Mean currents Equatorial Pacific from WOCE drifters')
ax[0].set_aspect('equal')
ax[0].set_ylim(-10, 12)
cs = ax[1].contourf(cenlon, cenlat, np.sqrt(Ustd**2 + Vstd**2), levels=50)
ax[1].set_aspect('equal')

cbaxes = fig.add_axes([0.11, 0.05, 0.8, 0.03])
cb = plt.colorbar(cs, cax = cbaxes, orientation='horizontal')

Now let’s try making zonal strips

cenlat1 = np.arange(-9.5, 9.6, 0.5)
Umean1 = np.nan * np.ones_like(cenlat1)
Vmean1 = np.nan * np.ones_like(cenlat1)
Ustd1 = np.nan * np.ones_like(cenlat1)
Vstd1 = np.nan * np.ones_like(cenlat1)

for ilat in range(len(cenlat1)):
    strip = np.where(np.absolute(drifters['lat']-cenlat1[ilat]) < 0.5)[0]
    Umean1[ilat] = np.nanmedian(drifters['u'][strip])
    Vmean1[ilat] = np.nanmedian(drifters['v'][strip])
    Ustd1[ilat] = np.nanstd(drifters['u'][strip])
    Vstd1[ilat] = np.nanstd(drifters['v'][strip])

And plot them

fig, ax = plt.subplots(1,4,figsize=(15,12), sharey=True)
q = ax[0].quiver(np.zeros_like(cenlat1), cenlat1, Umean1, Vmean1)
ax[0].quiverkey(q, -178, 11, 0.25, '0.25 m/s', coordinates='data')
ax[0].set_ylabel('Latitude')
ax[0].set_title('Mean currents from drifters')
#ax[0].set_aspect('equal')
ax[0].set_ylim(-10, 12)
cs = ax[1].plot(Vmean1, cenlat1, 'k')
ax[1].set_title('meridional current')
cs = ax[2].plot(Umean1, cenlat1, 'k')
ax[2].set_title('zonal current')
cs = ax[3].plot(np.sqrt(Ustd1**2+Vstd1**2), cenlat1, 'k')
ax[3].set_title('standard deviation')

Text(0.5, 1.0, 'standard deviation')

Pacific Variability- ENSO

There are several different indices for ENSO: https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni.

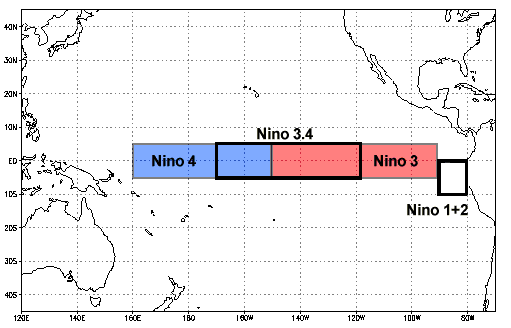
We use the Nino 3.4 index. The data are easily found online:

ninocols = ['year', 'month', 'sst', 'ssta', 'anom']
nino = pd.read_csv('https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/detrend.nino34.ascii.txt',
                    names=ninocols, delim_whitespace=True, skiprows=1)

nino

	year	month	sst	ssta	anom
0	1950	1	24.56	26.18	-1.62
1	1950	2	25.07	26.39	-1.32
2	1950	3	25.88	26.95	-1.07
3	1950	4	26.29	27.39	-1.11
4	1950	5	26.19	27.56	-1.37
...	...	...	...	...	...
861	2021	10	25.77	26.72	-0.94
862	2021	11	25.76	26.70	-0.94
863	2021	12	25.54	26.60	-1.07
864	2022	1	25.60	26.55	-0.95
865	2022	2	25.87	26.76	-0.89

866 rows × 5 columns

We need to fix the date; simplest way forward is:

date = nino['year'] + nino['month']/12

Let’s plot all the temperatures and anomalies, using the sharex argumnet to clean up the x-axes.

fig, ax = plt.subplots(3,1,figsize=(18,12), sharex=True)
ax[0].plot(date, nino['sst'], 'k')
ax[0].set_title('Nino 3.4 temperatures')
ax[1].plot(date, nino['ssta'], 'k')
ax[1].set_title('Nino 3.4 temperatures, climate-adjusted')
ax[2].plot(date, nino['anom'], 'k')
ax[2].set_title('Nino 3.4 anomalies')

Text(0.5, 1.0, 'Nino 3.4 anomalies')

Let’s zoom on last 30 years

fig, ax = plt.subplots(3,1,figsize=(18,12), sharex=True)
ax[0].plot(date, nino['sst'], 'k')
ax[0].set_title('Nino 3.4 temperatures')
ax[1].plot(date, nino['ssta'], 'k')
ax[1].set_title('Nino 3.4 climate-adjusted temperatures')
ax[2].plot(date, nino['anom'], 'k')
ax[2].set_title('Nino 3.4 anomalies')
for axis in ax:
    axis.set_xlim(1990, 2021.25)

Below is the code used to make the drifter file; you do not need to run it, but if you want to get a different sub-set of the data, you can change it to a code cell, modify it, and use it.

import pandas as pd import numpy as np import datetime # dates in days since 1 Jan year 1AD mindate, maxdate = datetime.datetime(1900,1,1).toordinal(), datetime.datetime(2022,1,1).toordinal() minlat, maxlat = -10, 10 minlon, maxlon = 165, 360-92 urls = ['ftp://ftp.aoml.noaa.gov/pub/phod/buoydata/buoydata_1_5000.dat.gz', 'ftp://ftp.aoml.noaa.gov/pub/phod/buoydata/buoydata_5001_10000.dat.gz', 'ftp://ftp.aoml.noaa.gov/pub/phod/buoydata/buoydata_10001_15000.dat.gz'] # list of names of columns colnames = ['id','month','day','year','lat','lon','sst','u','v','umag','latvar','lonvar','tempvar'] # make empty dataframe for appending just the data we want to keep to gooddata = pd.DataFrame([]) for ifile in urls: data = pd.read_csv(ifile, compression='gzip', delim_whitespace=True, names=colnames) # make date into ordinal number, days since 1 Jan year 1 date = np.array([datetime.datetime(yy, mm, int(dd)).toordinal() + dd%1 for yy, mm, dd in zip(data['year'], data['month'], data['day'])]) # find indices with each limit imindate = np.where(date>=mindate)[0] imaxdate = np.where(date<=maxdate)[0] iminlat = np.where(data['lat']>=minlat)[0] imaxlat = np.where(data['lat']<=maxlat)[0] iminlon = np.where(data['lon']>=minlon)[0] imaxlon = np.where(data['lon']<=maxlon)[0] # combine the indices, keeping only ones that satisfy both limits idate = set(imindate).intersection(imaxdate) ilat = set(iminlat).intersection(imaxlat) ilon = set(iminlon).intersection(imaxlon) # combine date, lat, and lon limits into a single list of indices # delete extra variables idata = sorted(list((idate.intersection(ilat)).intersection(ilon))) del imindate, imaxdate, iminlat, imaxlat, iminlon, imaxlon del date, idate, ilat, ilon # append data to new dataframe gooddata = gooddata.append(data.iloc[idata]) # save our new dataframe as its own csv file with gzip compression #gooddata.to_csv('/home/ocn463-data/woce/drift/pacdrift.gz', compression='gzip', index=False)